X and y are positive integers;Write a(x)/ b(x) in the form q(x) r(x)/ b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less than the degree of b(x), using inspection, long division,I am trying to solve the equation $$ (x^2y^2)y' 2xy = 0 $$ I have rearranged to get $$ y' = f(x,y) $$ where $$ f(x,y) = \frac{2xy}{x^2y^2} $$ From here I tried to use a trick that I learned Stack Exchange Network Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn,
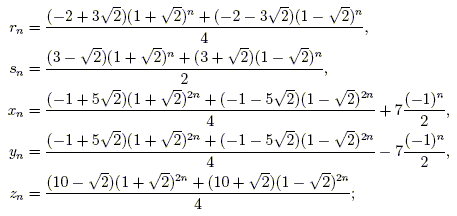
Pythagorean Triples
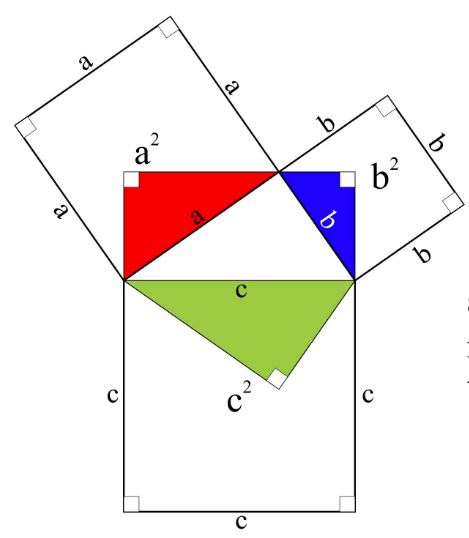
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 can be used to generate pythagorean triples
The identity (x^2 y^2)^2=(x^2-y^2)^2 (2xy)^2 can be used to generate pythagorean triples-The identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean The identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be generated using x = 8 and y = 3?Pythagorean triples are given by these formulas (x^2 y^2, 2xy, x^2 y^2) The length of one leg of a right triangle is 28 The lengths of the other sides are odd numbers Which of these numbers could be the length of the hypotenuse?




Pythagorean Triple Wikipedia
For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Rewrite rational expressions AAPRD6 Rewrite simple rational expressions in different forms;Use the Pythagorean identity, Latex (x^2y^2)^2(2xy)^2=(x^2y^2)^2\textsf{,} to create a Pythagorean triple Follow these steps Choose two numbers and identify which is replacing Latex x x and which is replacing Latex y\textsf{} How did you know which number to use for Latex x x and for Latex y\textsf{?} Explain how to find a Pythagorean triple using those numbers ExplainUse the Pythagorean identity, Latex (x^2y^2)^2(2xy)^2=(x^2y^2)^2\tex tsf{,} to create a Pythagorean triple Follow these steps Choose two numbers and identify which is replacing Latex x x and which is replacing Latex y\textsf{} How did you know which number to use for Latex x x and for Latex y\textsf{?} Explain how to find a Pythagorean triple using those numbers Explain
Generate Pythagorean Triples using an identity You'll gain access to interventions, extensions, task implementation guides, and more for this instructional video In this lesson you will learn to generate a Pythagorean Triple by using the identity (x^2 y^2)^2 (2xy)^2 = (x^2 y^2)^2The problem above requires us to do two things First, generate a Pythagorean TripleExplanation The function is f (x,y) = 2xy The partial derivatives are ∂f ∂x = 2y ∂f ∂y = 2x Therefore, dy dx = − ∂f ∂x ∂f ∂y = − 2y 2x = − y x Answer link(x 2 y 2) 2(2xy) 2The algebraic identities for class 9 consist of identities of all the algebraic formulas and expressions You must have learned algebra
Use the identity (x^2y^2)^2=(x^2−y^2)^2(2xy)^2 to determine the sum of the squares of two numbers if the difference of the squares of the numbers is 5 and the product of the numbers is 6 1 See answer shoppingwtia is waiting for your help AddCategories English Leave a Reply Cancel reply Your email address will not be publishedThe following identity can be used to find Pythagorean triples, where the expressions x2−y2, 2xy, and x2y2 represent the lengths of three sides of a right triangle;




Pythagorean Theorem How To Use Pythagoras Theorem With Examples




Pythagorean Triple From Wolfram Mathworld
Satyajeetdamekar004 satyajeetdamekar004 Math Secondary School answered Find the identity of x^2y^2 =?Categories English Leave a Reply Cancel reply Your email address will not be publishedWrite a(x) / b(x) in the form q(x) r(x)/b(x), where a(x), b(x), q(x), and r(x) are polynomials with the degree of r(x) less than the degree of b(x), using inspection,




Polynomial Identities Solutions Examples Videos Worksheets Games Activities




Mathematics For The Ib Diploma Analysis And Approaches Sl Draft Copy By Hodder Education Issuu
Answer (1 of 9) xy=2 (1) xy=?Find an answer to your question find the identity of x^2y^2 =?Simple and best practice solution for x^22xyy^2=x^2y^2 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it Equation SOLVE Solution for x^22xyy^2=x^2y^2 equation




Mathematics 2 Demo Scope And Sequence And 4 Sample Units By Grupo Anaya S A Issuu




Teaching Note Supply Tiles For Students A Apr 4 Objective Prove Polynomial Identities And Use Them To Describe Numerical Relationships For Example Ppt Download
Consider x^ {2}y^ {2}xy22xy as a polynomial over variable x Find one factor of the form x^ {k}m, where x^ {k} divides the monomial with the highest power x^ {2} and m divides the constant factor y^ {2}y2 One such factor is xy1 Factor the polynomial by dividing it by this factorUse the identity (x^2y^2)^2=(x^2−y^2)^2(2xy)^2 to determine the sum of the squares of two numbers if theChoose all that apply 45 53 65 195 197Solving Identity Equations An identity equation is an equation that is always true for any value substituted into the variable 2 (x1)=2x2 2(x 1) = 2x 2 is an identity equation One way of checking is by simplifying the equation 2 ( x 1) = 2 x 2 2 x 2 = 2 x 2 2 = 2 = 2x 2 = 2x 2 = 2 2=2 2 = 2 is a true statement



2



2
Simple and best practice solution for (xy)(x^22xyy^2)= equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it Equation SOLVE Solution for (xy)(x^22xyy^2)= equation$(w^2 x^2 y^2 z^2) = (a^2 b^2)$ What I am looking for is analysis an elegant algorithm to be applied in the general case, as opposed to specific cases eg where $(A^2 B^2)$ is below a certain numberChứng minh (x^2y^2)^2(2xy)^2=(xy)^2(xy)^2 chúng minh đẳng thức (x^2y^2)^2(2xy)^2=(xy)^2(xy)^2 Theo dõi Vi phạm YOMEDIA Toán 8 Bài 3 Trắc nghiệm Toán 8 Bài 3 Giải bài tập Toán 8 Bài 3 Trả lời (1) Ta có



How To Find Pythagorean Triplets With One Given Number Quora




Pdf The Modular Tree Of Pythagoras
And x>y calculus Use implicit differentiation to find an equation of the tangent line to the curve at the given point x2 2xy − y2 x = 17, (3, 5) (hyperbola) CalculusWrite an equation thatX and y are positive integers;



Www1 Cmc Edu



Pythagorean Triples Additive Problems And More Springerlink
Find dy/dx x^2y^2=2xy Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate Tap for more steps By the Sum Rule, the derivative of with respect to is Differentiate using the Power Rule which states that is where Evaluate Tap for more steps Differentiate using the chain rule, which states that is where and Tap3 Explain how to find a Pythagorean triple using those numbers 4 Explain why at leastAnd x>y maths 3x 14y = 5xy 21y x = 2xy kindly solve the pair of linear equation variation Can you please check my answers?
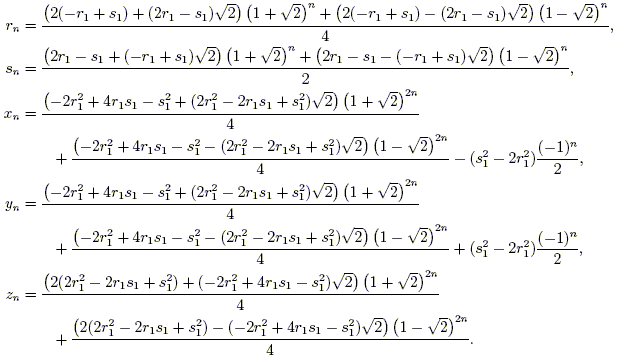



Pythagorean Triples



Resources Finalsite Net
Use the Pythagorean identity, (x^2y^2) (2xy)^2 = (x^2y^2)^2 , to create a Pythagorean triple Follow these steps 1 Choose two numbers and identify which is replacing x and which is replacing y 2 How did you know which number to use for x and for y?The identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean The identity (x^2 y^2)^2 = (x^2 – y^2)^2 (2xy)^2 can be used to generate Pythagorean triples What Pythagorean triple could be generated using x = 8 and y = 3?Correct answer to the question The identity (22 y2)2 = (x2 y2)2 (2xy)" can be used to generate Pythagorean triples What Pythagorean triple could be generated using 2 = 8 and y = 3?




Generating Pythagorean Triples Chilimath




Generating Pythagorean Triples 360
For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Suggested Learning Targets Understand that polynomial identities include but are not limited to the product of the sum and difference of two terms, the difference of two squares, the sum and difference of two cubes, the square of a binomial, etc ProveSimplify (xy)(x^2xyy^2) Expand by multiplying each term in the first expression by each term in the second expression Simplify terms Tap for more steps Simplify each term Tap for more steps Multiply by by adding the exponents Tap for more steps Multiply by Tap for more steps Raise to the power of Use the power rule to combine exponents Add and Multiply byPythagorean triples are given by the formula x^2y^2, 2xy, and x^2y^2 Use the formulas for the Pythagorean triples to find a right triangle with leg lengths of 16 and an odd number Show all of your work for full credit



Orange K12 Nj Us




A Apr 4 Objective Adding Amp Subtracting Polynomials Prove Polynomial Identities And Use Them
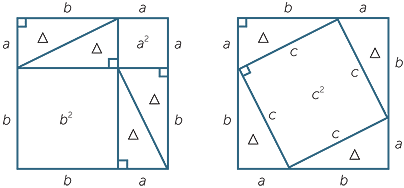
X 4 2x 2 y 2 y 4 = x 4 2x 2 y 2 y 4 (4x 2 y 2) combine like terms x 4 2x 2 y 2 y 4 = x 4 2x 2 y 2 y 4 combine like terms (x 2 y 2) 2 = (x 2 y 2) 2 (2xy) 2 so this Identity is always true This identity is used to create Pythagorean Triples For example, substituting x = 3 and y = 2The following identity can be used to find Pythagorean triples, where the expressions x2−y2, 2xy, and x2y2 represent the lengths of three sides of a right triangle;Identity (x2 y2)2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Desired Student Performance A student should know • Number theory • Consecutive numbers forms A student should understand • HowFor example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples With the increase in technology and this huge new thing called the Internet, identity theft has become a worldwide problem For this reason, it is paramount to keep important information such as addresses and telephone numbers as private as possible when



Generating Pythagorean Triples Chilimath



Pythagorean Triangles And Triples
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreNot a problem Unlock StepbyStep Extended Keyboard ExamplesSolution for (X^2y^2) (x^22xy) (x^2y^2) (y^2)= equation Simplifying (X 2 1y 2 ) (x 2 2xy) (x 2 1y 2 ) (y 2コレクション the identity (x^2 y^2)^2=(x^2y^2)^2 (2xy)^2 can be used X and y are positive integers;Example 5532 For the function f(x,y)=xy3, calculate the gradient at the point (2,1) and estimate z if x =1and y =2 Let's begin my finding the partial derivatives at (2, 1) • fx(x,y)=y3, which implies fx(2,1) = 1 • fy(x,y)=3xy2, which implies fy(2,1) = 6 Now, we may plug into



2




Pythagorean Identity Review Article Khan Academy
The identity (x^2 y^2)^2=(x^2y^2)^2 (2xy)^2 can be used to generate Satyajeetdamekar004 satyajeetdamekar004 Math Secondary School answeredUse the identity (x2y2)2=(x2?y2)2(2xy)2 to determine the sum of the squares of two numbers if the difference of the squares of the numbers is 5 and the product of the numbers is 6The following identity can be used to find Pythagorean triplesSTANDARD AAPRC4 AII Prove polynomial identities and use them to describe numerical relationships For example, the polynomial identity (x 2 y 2) 2 = (x 2 –y 2) 2 (2xy) 2 can be used to generate Pythagorean triples WORKSHEETS Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given (i) Area 25a2 – 35a 12 (ii) Areaコンプリート! the identity (x^2 y^2)^2=(x^2y^2)^2 (2xy)^2 can be used to generate pythagorean triples And x>y mathematics Pick a twodigit number greater than 25 Rewrite your twodigit number as a difference of two numbersX and y are positive integers;For example, see x4 y4 as (x2)2 (y 2 ) 2 , thus recognizing it as a difference of squares that can be factored as (x 2 y 2 )(x 2




Polynomials And Polynomial Functions Pdf Free Download




Pdf A New Approach To Generate Formulae For Pythagoreans Triples Quadruples And Their Generalisation To N Tuples
Consider , xy=0 (2) move y to RHS then its sign change '' to '' in eq(1) then, x=2yCorrect answers 2 question the identity (x^2y^2)^2 = (x^2y^2)^2 (2xy)^2 can be used to generate pythagorean triples what pythagorean triple could be generated using x=8 and y=3As others have pointed out x = 0 and y = 2 solves the first equation but definitely not the second which you can veryify but plugging it in Thus asking what x y x y is tricky because y has 3 different values However, it is 0 in all 3 because x = 0 in all 3 cases So we can say the answer is 0, but you are crossing the line a bit Let's




Teaching Note Supply Tiles For Students A Apr 4 Objective Prove Polynomial Identities And Use Them To Describe Numerical Relationships For Example Ppt Download




Mangahigh Review For Teachers Common Sense Education
For example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples 5 () Know and apply the Binomial Theorem for the expansion of (x y) n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined for example by Pascal's TriangleThe following identity can be used to find Pythagorean triples, where the expressions x2−y2, 2xy, and x2y2 represent the lengths of three sides of a right triangle;The previously listed algorithms for generating Pythagorean triplets are all modifications of the naive approach derived from the basic relationship a^2 b^2 = c^2 where (a, b, c) is a triplet of positive integers It turns out that Pythagorean triplets satisfy some fairly remarkable relationships that can be used to generate all Pythagorean triplets



The Pythagorean Theorem




The Identity X 2 Y 2 2 X 2 Y 2 2 2xy 2 Can Be Used To Generate Pythagorean Triples What Pythagorean Triple Could Be Generated
For example, the polynomial identity (x2 y2)2 = (x2 – y2)2 (2xy)2 can be used to generate Pythagorean triples D Rewrite rational expressions 6 Rewrite simple rational expressions in different forms;Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more




Calculus I Ii Amp Iii For Mahavier S Class Math Nerds



Pythagorean Theorem And Its Many Proofs



1




Pythagorean Triple Wikipedia




Pythagorean Theorem An Overview Sciencedirect Topics



1




Pythagorean Triple From Wolfram Mathworld



The Identity X2 Y22 X2 Y22 2xy2 Can Be Used To Gen Gauthmath




Pythagorean Theorem How To Use Pythagoras Theorem With Examples



Pythagorean Triangles And Triples




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download



Times Module M15 Pythagoras Theorem



How To Find Pythagorean Triplets With One Given Number Quora




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download




Pythagorean Triples Video Lessons Examples Step By Step Solutions




Polynomial Identities And Pythagorean Triples Activity Polynomials Algebra Resources Algebra 2 Activities



2



1



Pythagorean Triples



Arxiv Org




The Modular Tree Of Pythagoras Citeseerx




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download




Pythagorean Triplet In An Array Geeksforgeeks



Symbolic Computation All You Ll Ever Need To Know About Maple J J O Connor A P Naughton Pdf Free Download



Pythagorean Triple From Wolfram Mathworld




Pythagorean Triple Wikipedia




Pythagorean Triple From Wolfram Mathworld




Pdf Pythagorean Triples Before And After Pythagoras Ravi Agarwal Academia Edu




Problem 1 Multiples Of 3 And 5 Problem 2 Even Fibonacci Numbers Manualzz




Formulas For Generating Pythagorean Triples Wikipedia




Pythagorean Theorem An Overview Sciencedirect Topics



Times Module M15 Pythagoras Theorem




Pdf Pythagorean Triples Before And After Pythagoras



Pythagorean Triangles And Triples




Pythagorean Theorem An Overview Sciencedirect Topics



Pythagorean Triples




Pdf Pythagorean Triples Before And After Pythagoras




View Question End Of Day Wrap




Aim How Do We Use Structure To Prove Find Pythagorean Triples Ppt Download




Answered Show That X Y X Y Bartleby




Polynomial Identities And Pythagorean Triples Activity By Math Beach Solutions




Pdf Redefining And Classifying Primitive Pythagorean Triples Benomatics Edunoid Academia Edu




Pythagorean Triples Generator Youtube



The Pythagorean Theorem
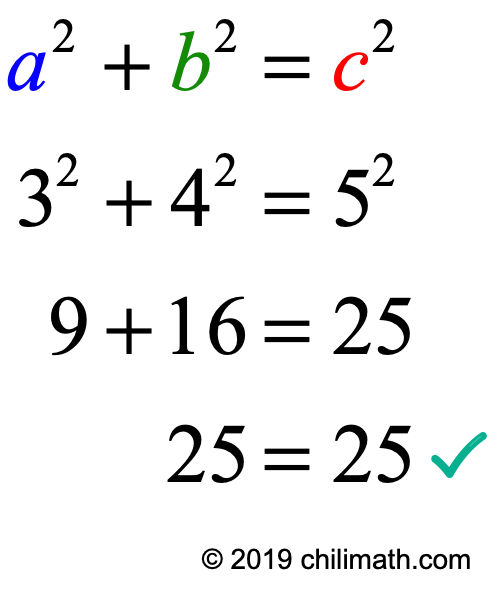



Generating Pythagorean Triples Chilimath




Answered Example 3 Jeremy Uses The Polynomial Bartleby



2



Pythagorean Triple Wikipedia
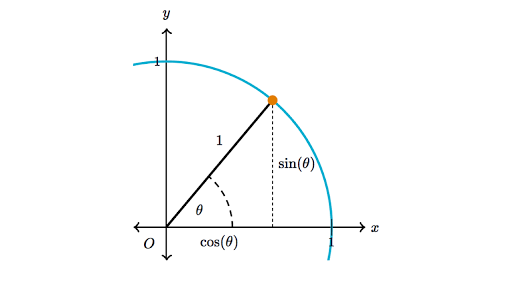



Pythagorean Identity Review Article Khan Academy




How To Use The Pythagorean Theorem With A Circle Veritas Prep




The Academy Corner Dong Thap In South Vietnam Portal Manualzz



Math Lsu Edu




Lesson 10 The Power Of Algebra Finding




6 The Abc S Of Number Theory




Gmat Triangles Archives
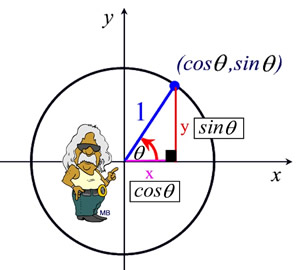



Pythagorean Identities Mathbitsnotebook Ccss Math



How To Find Pythagorean Triplets With One Given Number Quora
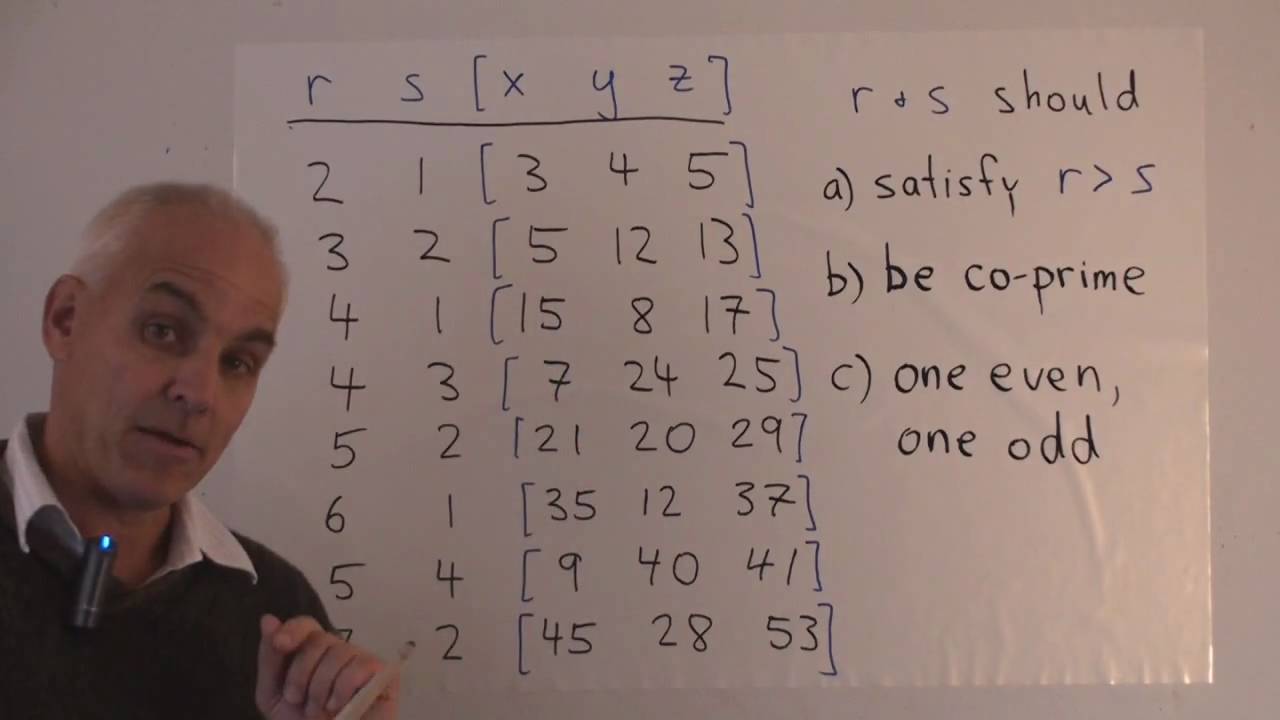



Pythagorean Triples Explanation Examples




Unit 6 A Pythagoras Sides Of Squares Rusmp Geometrymodule Pdfdocuments Pythaآ Trainer Instructor Pdf Document




Pythagorean Triple Wikipedia




The Get It Guide Review For Teachers Common Sense Education



Pythagorean Triangles And Triples




900 Algebra 2 Ideas Algebra 2 Algebra Lesson Plans



1




Use The Pythagorean Identity X2 Y 2 2xy 2 X2 Y2 2 To Create A Pythagorean Brainly Com
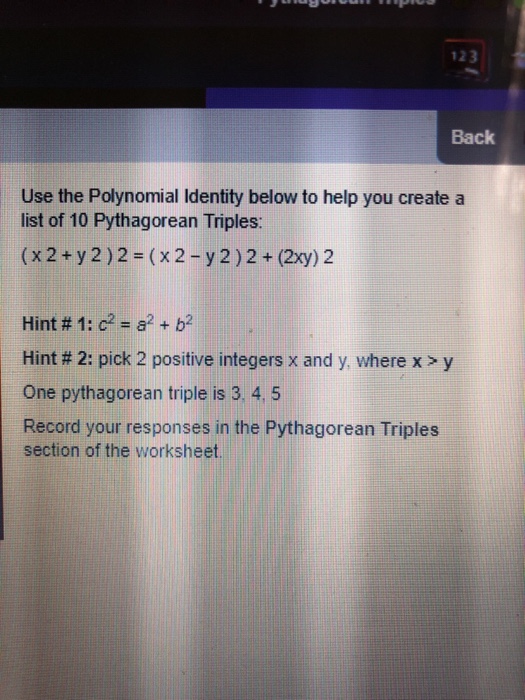



Solved 123 Back Use The Polynomial Identity Below To Help Chegg Com



2




How To Use The Pythagorean Theorem With A Circle Veritas Prep



Jstor Org




Pdf Postprint Of Some Relations Among Pythagorean Triples
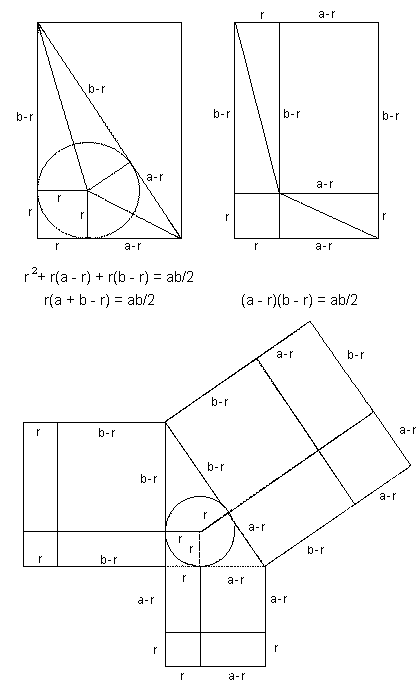



Pythagorean Theorem And Its Many Proofs




Use The Pythagorean Identity On Page 10 With X 4 And Y 3 To Generate A Pythagorean Triple Brainly Com



Math Questions Math Answers



Pythagorean Triangles And Triples




Generate Pythagorean Triples Using An Identity Learnzillion
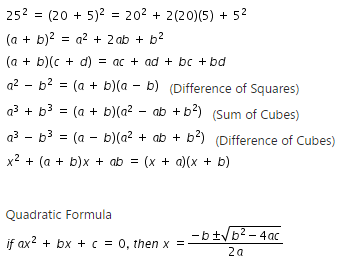



Mafs 912 A Apr 3 4 Prove Polynomial Identities And Use Them To Describe Numerical Relationships For Example The Polynomial Identity X Y X Y 2xy Can Be Used To Generate Pythagorean Triples



0 件のコメント:
コメントを投稿